
Mishita Dharia - Quadratics
Multiplying Binomials and Special Products
A binomial is a polynomial with two terms.When multiplying two binomials together, you expand and simplify, using FOIL. This stands for First Outside Inside Last.
Let’s do an example…
If we have two binomials (3x + 2)(4x + 4) we would first multiply the 3x with the 4x and 4, then we would multiply the 2 with the 4x and the 4, and then finally we would simplify by adding the like terms.
(3x + 2)(4x + 4)
= 12x^2 + 12x + 8x + 8
= 12x^2 + 20x + 8
Now you try…
Multiply the binomials (2x – 4)(3x + 5)
Answer…
6x^2 - 2x - 20
Extra Practice…
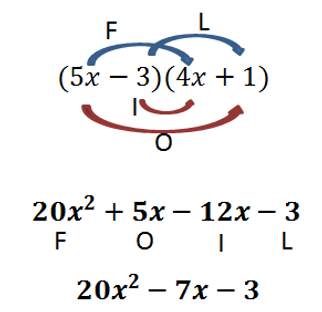
Special Products: There are a couple times where there are easier ways to find the product of two binominals than multiplying each term in the first binomial with the terms in the second binomial. These two types of special cases when multiplying binomials are difference of squares and complete squares.
Complete Squares:
Investigate...
What happens when we square a binomial?
(3x + 5)^2
= (3x + 5) (3x + 5)
= 9x^2 + 15x + 15x + 25
= 9x^2 + 30x + 25
This is equivalent to…
= 9x^2 (2*3*5*x) + 5^2
So…
(a+b)^2 = a^2 + 2ab + b^2 or (a-b)^2 = a^2 - 2ab + b^2.
The sign in front of the middle term will always correspond to the sign in the binomial equation.
Now you try…
What do you get when you square the binomial (2x – 6)^2
Answer…
= 2x^2 + 24x + 36
Difference of Squares:
Investigate...
What happens when we multiply (x+4)(x – 4)?
(x+4)(x – 4)
= x^2 + 8x - 8x + 16
= x^2 + 16
This is equivalent to…
= x*x*4*(-4)
So…
(a+b)(a−b) = a^2 – b^2
Now you try…
What do you get when you multiply (x + 8)(x - 8)
Answer…
= x^2 – 64
Extra Practice…