Mishita Dharia - Quadratics

When graphing a parabola in standard form, it requires two very important things the x-ints and the vertex. You should already know how to find the x-ints for an equation in standard form (if not review the lesson on finding the zeros in standard form). Now if you want to find the vertex, you need to do two things, first find the axis of symmetry (which we all know is the h-value in the vertex) by adding the x-intercepts and then dividing the sum by 2. Next we have to find the k value (or the optimal value) of the vertex, and we can do this by subbing in the axis of symmetry in the equation, and solve for y. When we have our three points we can plot them on the graph and draw a line through them.

 

Let’s do an example…

 

Graph the following equation y = x^2 - 9x + 20

 

This is a simple trinomial so the factored from of this is…

y = (x-4)(x-5)

 

Because… (-4)x(-5) = 20 & (-4) + (-5) = -9

 

Then we have to find the x-intercepts by first subbing in 0 for y and then setting each bracket equal to zero.

0 = (x-4)(x-5)

(x-4) = 0

(x-5) = 0

 

Then we remove the brackets and solve for x.

x – 4 = 0

x = 4

 

x – 5 =0

x = 5

 

Now, to find the axis of symmetry we must add the two x-ints and then divide by 2.

A.O.S = (4+5)/2

A.O.S = 9/2

A.O.S = 4.5

 

We then have to find the k-value. In order to do this we must sub in 4.5 for x into the original equation of y= x^2 - 9x + 20.

y= x^2 - 9x + 20

y= (4.5)^2 – 9(4.5) + 20

y= (4.5)^2 – 9(4.5) + 20y= 20.25 – 40.5 + 20

y = (-0.25)

 

Therefore the vertex is (4.5, -0.25)

 

 

 

 

Now you try…

Graph the following equation y=2x^2-8x+6

 

**Remember this is a complex trinomial so it must be factored as a complex trinomial. (Refer back to the lesson on solving complex trinomials).**

 

Answer…

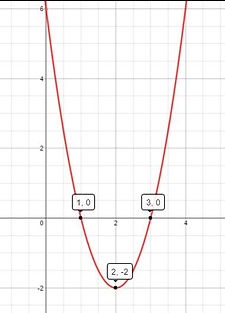
X intercepts: (1,0) & (3,0)

Vertex: (2, -2)

 

Your Graph Should Look Like this:

 

 

 

 

 

 

 

 

 

 

 

Extra Practice…

 

 

 

 

 

 

 

 

 

A Video for Extra Help…