Graphing Quadratics in Vertex Form

Graphing Quadratics using Step Pattern and Mapping Notation

Mapping Notation: an algebraic method to find new key points of a transformed parabola.

The basic formula for a parabola is y = x^2, this means that the equation has a vertex of (0,0) since there is no k or h-value in the equation (no transformations are applied).

Let’s make a table for the x and y-values for y = x^2…

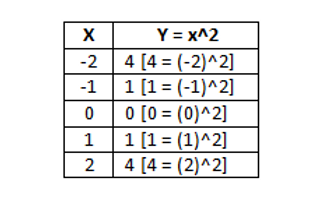
Question…

If the value of x is 6 than what would the y value be?

Answer…

36 because 36 = 6^2

Let’s describe the transformations for y = 2(x-7)^2 - 5…

a = 2, vertical stretch and opens up, therefore multiply y-values by 2.

k = 5, vertical translation 5 units down, therefore subtract 4 from y.

h = 7, horizontal translation 7 units to the right, therefore add 3 to x-values.

Let’s see how the transformations above affect the x and y coordinates of the key points of the graph y = x^2…

How do the values of a, h, k affect the x, and y coordinates of the key points of the graph y=x^2?

The a-value affects the y coordinate of the graph, so to find the transformed point you must multiply the value of a with the y coordinate.

The h-value affects the x coordinates of the graph, so to find the transformed point you must add the value of h to the x coordinate.

The k-value affects the y coordinate of the graph, so to find the transformed point you must add the value of k to the y coordinate.

So…

We can apply the transformation properties and algebraically define a mapping form from y=x^2 to y = 2(x-7)^2 – 5 as: (x, y) (x+h, ay+k)

Let’s do an example…

Write the mapping formula for y = 5(x - 2)^2 + 3

Identify the a, h, and k values, then sub them into the equation (x+h, ay+k).

a=5 h=2 k=3

(x, y) (x+2, 5y+3)

Now you try…

Write the mapping formula for y = – 2x^2 + 6

Answer…

a = -2 h = 0 k = 6

(x, y) (x, -2y+6)

Now we can use this formula to determine the transformed “key points” and to graph an equation…

Write the mapping formula and graph the equation = 2(x – 4)^2 + 5

a = 2 h = 4 k = 5

(x, y) (x+4, 2y+5)

Now you Try…

Write the mapping formula and graph the equation y = 0.5(x + 4)^2 – 3

Answer…

(x, y) (x-4, 0.5y-3)

Step Pattern: You can also use step progression to the sketch the graph of an equation.

The step pattern consists of identifying and plotting the vertex, determining the step pattern, plotting the step points, reflecting each point across the axis of symmetry, and then drawing a smooth curve between the points.

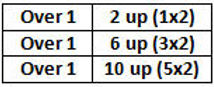
The step pattern is…

Let’s do an Example…

Graph the quadratic relation y = x^2 where a=1 using the step pattern.

The vertex is (0,0) it would open up since a = 1, and so from there we would go…